Il PageRank di Google

Come si calcola il PageRank

Ecco cosa dice Google: "PageRank or PR(A) can be calculated using a simple iterative algorithm, and corresponds to the principal eigenvector of the normalized link matrix of the web".

Questo significa, in parole povere, che noi possiamo ugualmente procedere, e calcolare il PageRank di una pagina, ANCHE senza conoscere il valore finale del PageRank delle altre pagine: ogni volta che il calcolo viene iterato, esso si avvicina approssimativamente sempre più al valore definitivo, e l'iterazione continua fino a quando tutti i calcoli si esauriscono e i valori smettono di cambiare. L'algoritmo iterativo si avvicina cioè al valore definitivo per successive approssimazioni.

Prendiamo il caso più semplice: due pagine che si linkano a vicenda, che chiameremo Pagina A e Pagina B. Ognuna di queste due pagine ha quindi un link in uscita. Dato che ogni link vale 1, quindi C(A)=1 e C(B)=1.

Noi non sappiamo acora da dove parte il loro PageRank, quindi supponiamo che sia 1.
d=0,85 come abbiamo visto.
Ora, prendiamo la formula:
PR(A)=(1-d)+d(PR(T1)/C(T1)+ ... +PR(Tn)/C(Tn))
che per la pagina A diventa:
PR(A)=(1-d)+d(PR(B)/C(B))
quindi:
PR(A)=(1-0,85)+0,85(1/1)
PR(A)=1-0,85+0,85=1
Lo stesso vale per la pagina B:
PR(B)=1-0,85+0,85=1

Supponiamo invece di fissare il PageRank a zero. Ecco cosa accade.
Prendiamo di nuovo la formula:
PR(A)=(1-d)+d(PR(T1)/C(T1)+ ... +PR(Tn)/C(Tn))
che per la pagina A diventa:
PR(A)=(1-d)+d(PR(B)/C(B))
quindi:
PR(A)=(1-0,85)+0,85*0
PR(A)=0,15+0=0,15
A questo punto, ecco invece cosa accade per la pagina B:
PR(B)=(1-d)+d(PR(A)/C(A))
quindi:
PR(B)=(1-0,85)+0,85(0,15)
PR(B)=0,15+0,12=0,27

Ripetendo l'iterazione più volte, cioè, entrambi i valori continuano a cresecere essendo dipendenti dalla crescita reciproca. Quando l'iterazione termina, entrambi i PageRank saranno unguali a 1.
Ma cosa accade se assumiamo come valore iniziale un valore superiore a 1? In questo caso, noteremo che l'iterazione, anzichè al rialzo, opera al ribasso, fino ad avvicinarsi a 1!

Non importa da quale punto casuale si parta: una volta che si avvia l'iterazione del calcolo del PageRank, la distribuzione normale, cioè la media del PageRank per tutte le pagine sarà sempre uguale a 1.

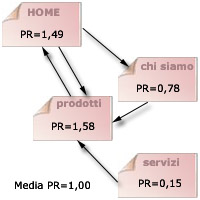
Quante volte abbiamo bisogno di ripetere l'iterazione in una grande rete come il web? Può darsi milioni di volte. Basti pensare che per sviluppare l'esempio qui a fianco, semplicissimo, abbiamo bisogno di 20-40 iterazioni. la pagina PRODOTTI ha il PageRank più alto, in quanto beneficia di tre link in ingresso, ed ha un solo link in uscita, a differenza della homepage che ha un link in ingresso e uno in uscita. Nella realtà, considerato il basso valore della homepage, una struttura di questo tipo sarebbe scorretta. La pagina SERVIZI è, quella con PageRank più basso, in quanto ha un link in uscita e nessun link in ingresso. Ogni pagina, anche priva di link, ha in teoria un valore minimo di 0,15 da condividere.

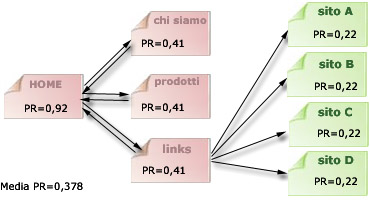
Ecco invece una semplice gerarchia con alcuni link in uscita verso l'esterno e il PageRank calcolato. Ora, la homepage ha il PageRank più corretto, ma che cosa è accaduto al PageRank medio? E' diminuito drasticamente. Questa diminuzione è stata provocata dalla dispersione di link verso l'esterno, che non va a detrimento della pagina che li dispensa, ma di tutto il sito.

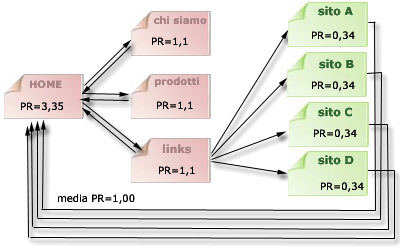
Poniamo che i link esterni restituiscano il favore, ma anzichè alla pagina chiamante, alla homepage del sito di partenza: in questo caso, la media complessiva dei due siti torna a 1, ma il PageRank della homepage balza a 3,35, e comunque il sito chiamante supera 1 anche nelle pagine interne.